Investigating Land Value Tax Rates
What are we taxing when land value approaches zero, and why is it possible to have tax rates above 100%?
When people first learn about the idea of a land value tax, they often wonder what the tax rate should be, and what the effects of different rates are. The central Georgist idea is to capture land rent, but determining this can be difficult, since we generally only have information about the sale value of land. If we tax sale value, then that in turn has the effect of lowering the sale value, because there’s less rent that would go to the owner. How do we make sense of this interdependence, and what happens at different tax rates? We’ll use a little bit of algebra, but it’s not necessary to follow it to understand the conclusions we reach.
(Note: It appears that Substack shows the source for the equation blocks when you select text anywhere. Reload the page to restore them.)
As a refresher, Georgist principles are based on the idea that you are entitled to the value produced by your own labor, and that natural resources, which are not created by anyone, are the common property of all. Land encompasses all of the natural resources you need to survive, and if somebody can deny you the use of it, they can force you to give them all of the value you produce, in the form of rents. According to Georgism, most of the concepts of landownership and personal domain over pieces of land are all still reasonable, but landowners are obligated to compensate society for the land they hold in order to nullify this monopoly power, the inequality it creates, and its stunting effects on the economy. With this view, the landowner is actually a tenant, occupying land which is collectively owned by everyone. The rent the landowner owes the public is most readily implemented as a tax, levied on the value of the land they occupy, but not the improvements they make to the land through their own labor. This is the land value tax.
As our example, let’s consider a plot of land with a residence on it in the middle of a city. Every year, the residence generates $100,000 worth of rents due to its favorable location, where it’s close to jobs, restaurants, and cultural amenities. There are additional costs to maintain the building in working condition, pay off the loan used for its construction, and the like, so the total rents received from the tenants are higher by these costs, but we won’t worry about this. We’ll just assume the land itself generates $100,000 of value without labor each year for the owner, and we’ll only consider the value of the land itself excluding the building on top of it. This $100,000/year is the productivity of the land, and is the land rent.1 We’ll call this land rent RL. Without any tax, all of the land rent is taken by the owner. We’ll call the rent the landowner takes RO, and in this case RL=RO.
When we introduce a tax on the land, levied each year, this tax is taken from the total land rent, reducing the amount that goes to the owner. We’ll call this tax RP, for the rent that is taken by the public. The total land rent is now split between the public and the owner.
To put it another way, the amount of rent the owner takes is the total land rent less the amount taken by the public with the land tax.
Taxing Land Rent
Let’s assume we know what RL is, and we can directly tax land rent and not land value. We just pick our tax rate x, which is somewhere in the range of 0–100%, and the rent to the public is
Now, the rent the owner takes is less by this amount.
Now we can divide both sides by RL to get the fraction of the total land rent taken by the owner, which is RO / RL.
In graphical form, this is a straight line. The horizontal axis is our tax rate, and the vertical axis is the fraction of the total land rent that goes to the owner. We’ll explain why in the next section, but the value of the land is proportional to the rent the owner takes, RO, and so the sale value of the land follows this same trend, going to zero as the owner’s rent goes to zero. To make the graph less cluttered we’ve only labeled the y axis as the relative land value, but it is the very same graph for relative owner’s rent, which is what we actually solved for.
Now, if we just knew what the land rent RL was, implementing a land tax would be easy. We would just set the tax, RP, to whatever fraction of RL we wanted. We could set them to be equal, capturing all of the land rent for the public and causing the rent the landowner receives without labor to fall to zero. Georgism achieved!
But not so fast. The land rent RL is difficult for an outsider, such as a tax assessor, to determine without detailed information about the land and housing market conditions. The people with the most knowledge of the land rent are those who are already operating businesses on similar land, or who want to start doing so. We can use this information by basing our tax on the sale value of land.
Taxing Land Value
Let’s say the owner of the land wants to retire, and puts the lot up for sale. Since the land is well suited for housing, the most interested buyers are those who want to operate rental businesses themselves. When assessing the value of the location, they use their own knowledge of the housing market to place what they believe are reasonable bids for the land. Thus activity in the market for land produces information about the value of land, using the local expertise of the people that want to use it. What will buyers consider the value to be?
A buyer will want to recoup the cost of their purchase within some time horizon. Nearly all land purchases are done using loans, and the new owner will want to pay off the loan within some number of years (we’ll ignore interest here). The amount that the owner will be able to recoup each year is the rent the owner is able to take for themselves, RO. Thus the value of the land to the owner, which we’ll call VO, is the annual rent to the owner multiplied by the time horizon in years. We’ll call it T and assume T is 10 years.
Here we see how RO is directly proportional to VO, as we mentioned earlier. If the rent the owner can take is halved, then the value of the land is halved as well. We can consider the land as having a total value VL, which is the total land rent multiplied by the time horizon.
This version of the land value doesn’t change, since RL and T are fixed. But what does change if we introduce a tax is the value to the owner, VO, and this is what we’ll call the land value. This is also the sale value.
When there is no tax, RO=RL, and VO=VL. Dividing the VL equation from the VO equation, we see that the relative land value, VO/VL, compared to the no tax case, is equal to the fraction of the total land rent taken by the owner, RO/RL.
Now, let’s see what happens if we set our tax, RP, to a fraction of the land value, VO.
Starting again with the owner’s rent in terms of the total rent and the public’s rent (tax), we solve for the fraction of the total rent the owner takes, RO / RL, as a function of the tax rate x.
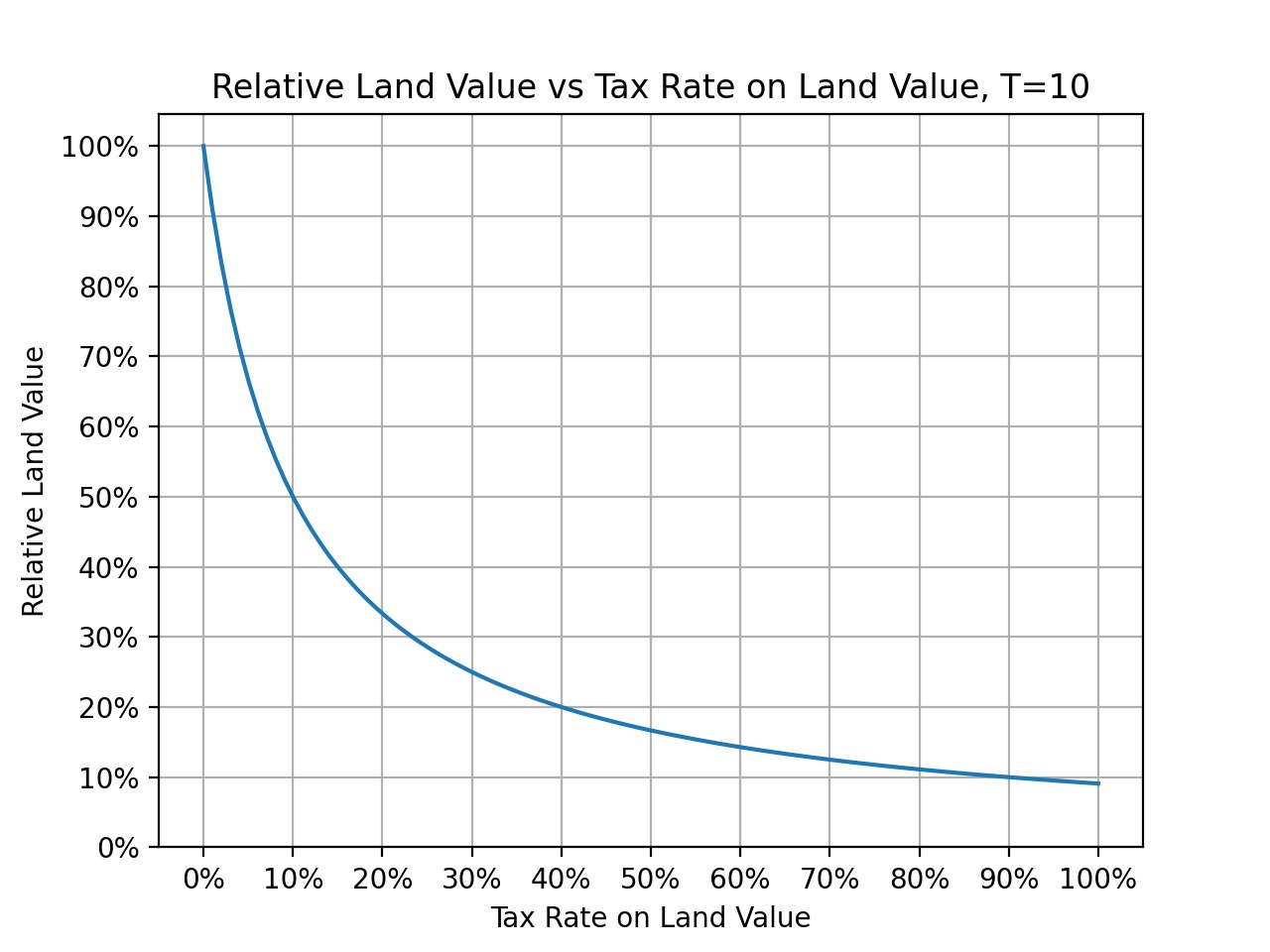
Plotting this out graphically with a time horizon T of 10 years, we can see the effect of the tax rate on the value of land. The amount of rent that goes to the owner follows the same curve as the change in land value.
Here is an interactive plot where you can change the time horizon.
Let’s go back to our example. We’ll still assume a 10-year time horizon. With no tax, all of the land rent is taken by the owner. At a land rent of $100,000/year, the land value is $1,000,000. Now let’s introduce a land value tax rate of 10%, levied each year. According to our calculations, the land value would drop to 50%, and would be $500,000. Every year, the owner would pay 10% of this land value each year in taxes, which would be $50,000/year. Over 10 years, this adds up to $500,000 paid to the public. In the same amount of time, the owner takes for themselves the remaining $500,000 from the total land rent, and this matches the land value.
We can see how small land value tax rates can have large effects, especially in land markets with long time horizons. In the 10-year case, only a 10% land value tax is required to capture half of the land rent! This is perhaps part of why implementing land value taxes is so difficult in the first place. Most of the big changes occur early on. Selling people on a small land tax pretty much requires selling them on the full thing.
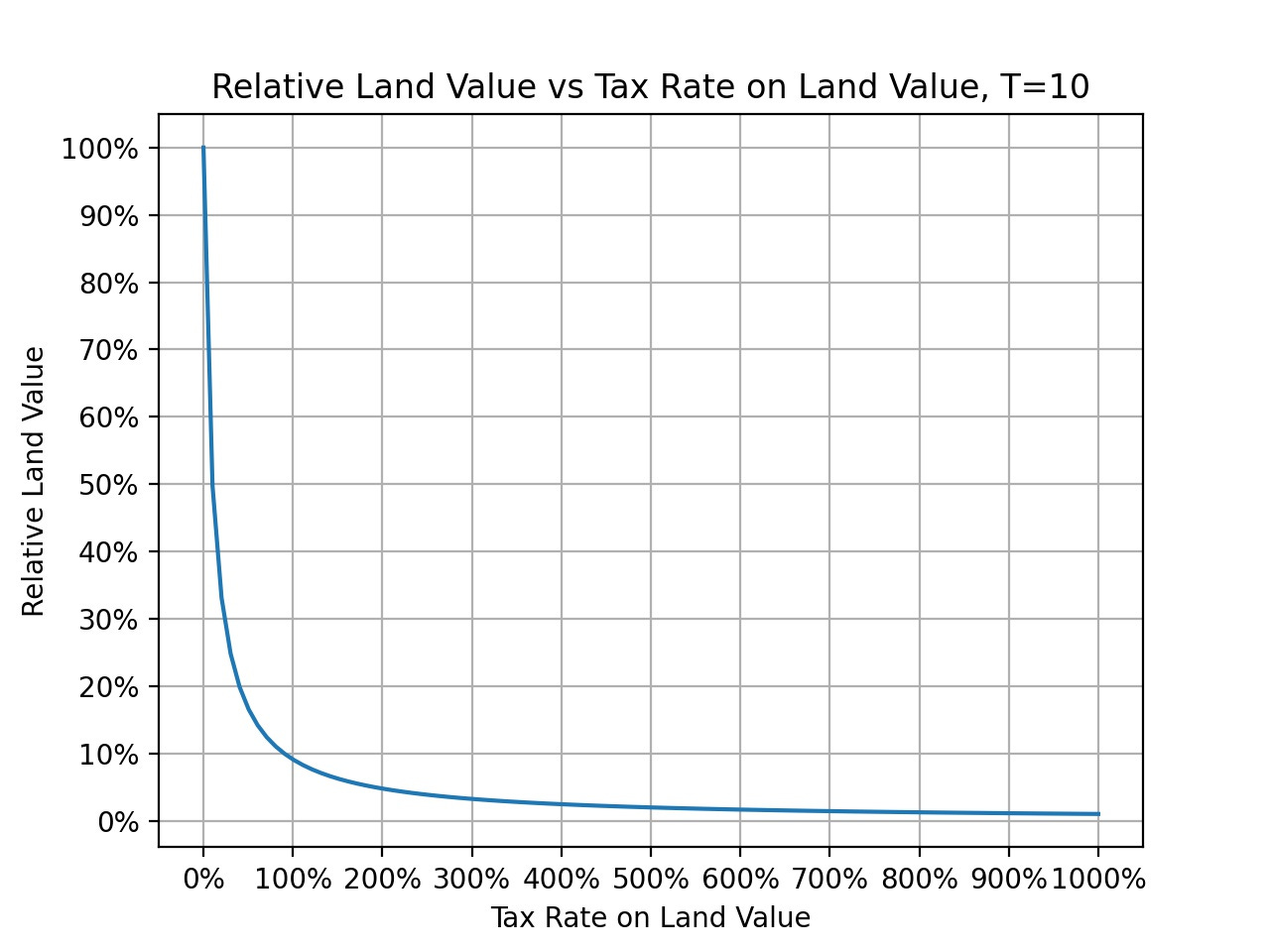
One neat thing about taxing the sale value of land is that we’re not at risk of taxing at too high of a rate. There’s not some cutoff at 100% where everything breaks. You’ll notice that the land value is still at 9% at this point. This is because sale value is based on the amount of rent the owner takes for themselves, which has to be nonzero if the land value is nonzero. This means that tax rates well over 100% are possible, since this just shrinks the land value closer to zero, giving a larger fraction of the land rent to the public and less to the owner. There is no finite tax rate on land value that would capture all of the land rent, but larger tax rates get closer. Here’s the same plot, but with a bigger range of tax rates displayed.
As u/timerot pointed out, there’s another, more intuitive, way of seeing the relationship between the owner’s time horizon and the tax rate on land value. If we take the inverse of the time horizon T, we get what’s called the capitalization rate. This is the rate at which the owner takes rent from the land, as a fraction of the land value. We’ll call this c, and it’s defined as
A 10-year time horizon would be the same as a 10% annual cap rate. With this our owner’s land value equation
becomes
This resembles the public’s rent, which was
Because the owner’s rent and the public’s rent add up to the total land rent, we can solve for the relative owner’s land rent, RO/RL.
The owner and the public both take rent from land each year as a fraction of the land value, at rates c and x. If we divide the owner’s capitalization rate c by the total rent rate c + x, we get the ratio of the owner’s rent to the total land rent, which is the same as the relative land value.
In our example, the cap rate is 10% and the land tax is 10%. Dividing 10% by 20% gives us 1/2, which is the relative land value we found earlier. Pretty neat!
Rent is actually the productivity of land relative to alternatives. The simplest alternative to consider is the margin of cultivation, where land is so much less productive that nobody wants to use it, and the rent is zero. In urban locations, land value is mainly due to city infrastructure and proximity to services. Rents would be much lower out in the countryside where none of these are available.





i always a appreciate some georgist math! having to refresh to fix the formatting is annoying. oh well.